Tuesday April 21, 2020, the Youtube channel 3Blue1Brown streamed a lesson using the unit circle to derive the half-angle formula of trigonometry. Let’s learn how he derives the world’s most famous trig identity: sin² Θ + cos² Θ =1 . It is not the usual method!
The right triangle has been used for thousands of years in construction (think of EGYPT’s pyramids). We use it still today for many real world problems. (Buildings, bridges, electrical devices etc.) Tell me how you use it in the comments below.
Let’s begin with a right triangle (see my diagram) and then also create two more right triangles, but inside the first one! How. Start at the vertex of the right angle and carefully draw a segment to the opposite side but it must make a right angle with that side. You may need to use a straight edge and try it a few times.
Here is what you should have. Label your points like mine , please.

The Largest triangle and the smaller triangle both share angle A and they each have a right angle thus these two triangles are SIMILAR. And we see for the largest triangle and triangle DBC that they share angle B and have right angles too. They too are similar. Thus all three triangles are similar and that means their corresponding angles are congruent (equal measures). For example: angleACD=angleB and angleBCD=angleA. Do you recall how to “mark” congruent angles?
Now to the video, finally. (Begin watching at 1 hour 5 minutes.) He used this triangle to discover a truth about sine and cosine. We call them identities because they are true for all numbers that can be used in the equation. USUALLY we just find a few numbers or no numbers that make an equation TRUE.
First he stated measure of segment AB, largest hypotenuse in our diagram = 1. Write that on your diagram. I can write another lesson if you like (explain why SIDES are cosΘ and sinΘ – weird notion to describe sides!); I will use the other info he discovered about his chosen angle, theta. MY “focus” angle above is angleA; mark it with theta, Θ, or darken it. It is our focus. He stated measures for sideAC = cosΘ and then sideBC= sinΘ. Write that and sideAD=s and sideDB=s’. Write that too.

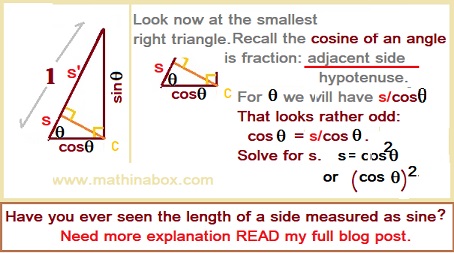
Now LOOK at just the smaller triangle. Recall the cosine of an angle is fraction: (adjacent side)/ (hypotenuse). Middle part of SOH-CAH-TOA.
Looking at my smaller triangle above, cosine of our Θ is s/cosΘ .
That looks rather odd:
cos Θ = s/cosΘ , yes, it is correct.
Solve for s. s= (cosΘ) ² or s= cos² Θ . NOW do same process for the s‘, called s prime in math (just a name we like!). But that requires knowing the angle DCB (oops- I erased those letters- look back at first diagram). We do know it since the triangles are SIMILAR. It too is Θ. You will have sin Θ = s’/sinΘ and that becomes s‘ = (sinΘ) ² or s‘ = sin² Θ .
Wow, that is a lot of geometry and a little bit of trig! ONE last comment and it is about the identity he was “discovering”. RECALL the 1 we used for the largest hypotenuse. That was the only number we used because we see it on the unit circle.
Did you read that lesson about the unit circle? NOW, we know, by looking at the long hypotenuse, that s + s’=1. BUT, what did we just find for s and s‘? We can use substitution (more geometry words!) and have cos² Θ + sin² Θ =1.
Or, its most famous way is to write the sine first: sin² Θ + cos² Θ =1
Send me your questions. And watch for their next video on April 24, 2020. YouTube channel 3blue1brown. I could write many more lessons on this one video. WHAT is your suggestion/comment? What typos did I make?
Do you recall the half angle identity for cosine? If we know cosA is 0.5000 then what is cos(A/2)? Hope you don’t think it is half of the 0.5000. NO calculator use, please.