Lockdown Math ep3: Is “i” Real-ly an Imaginary number?

The complex number system is comprised of real numbers and the imaginary numbers. 3+4i or i√2 or 4 or 0 or -100i or -1+i are examples of complex numbers. They can have an imaginary part and also real part (3+4i or -1+i). But they can also be only real (4 or 0) or only imaginary (-100i or i√2). We can add/subtract complex number much the same way we add/subtract like terms in algebra. We can multiply them using the distributive property, again much like algebra except we need to recall the DEFINITION of “i”, which is what we use to indicate imaginary numbers. The definition is simple: i²= -1.

Notice for Multiplication:

1. if z is complex number then z times 1 is z
2. if z is complex number then z times i is zi and will be perpendicular to z, that is, zi is found by rotating z 90 degrees counterclockwise.
3. if z is complex number then z(c+di). [where c+di is another complex number], will be cz + d(zi). Notice we have z (from step 1 above) multiplied by c and the zi (from step 2 above) multiplied by d.

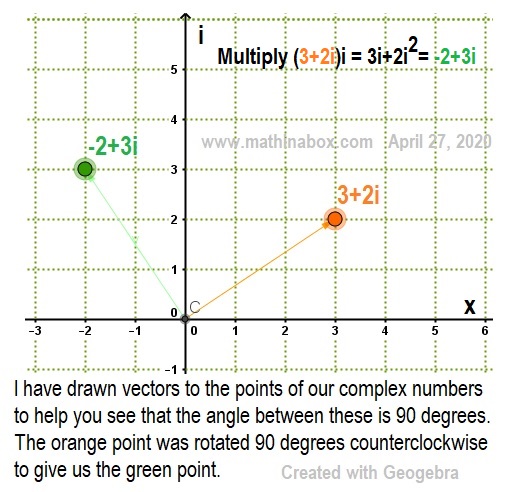
Let us look at these graphically. Recall the x and y axes are perpendicular ( make 90 degree angle). And from note 2 above, the z and zi are perpendicular. We will see example of this in a moment. Thus the idea was presented to let the y-axis be the “i” axis since z and zi are perpendicular. This gives us a way to graph complex numbers. Look at 3+2i and also -2+3i. I think you will see the 3+2i has been rotated 90 degrees in the counterclockwise direction and gives us -2+3i. And from NOTE 2 above, let us multiply the 3+2i by i: (3+2i)i = 3i +2i² which is 3i +2(-1) or -2+3i.

When we multiply by i the new number will be rotated 90 degrees counterclockwise. Look at the graphs of 3+2i and -2+3i.

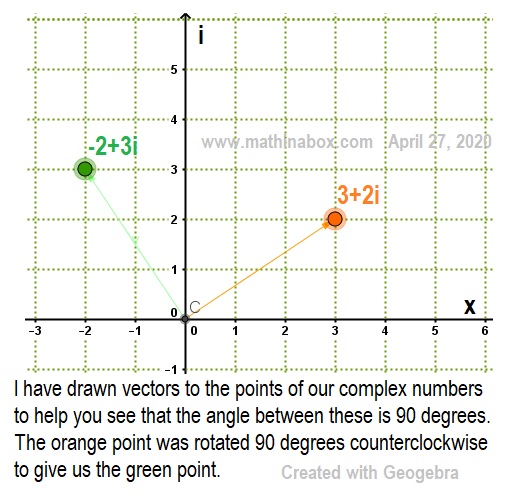
You can also use the slopes of the vectors to prove they create a right angle. The product of their slopes will = -1 if they are perpendicular. What is the slope of the orange vector? What is the slope of the green vector? Multiply and you should get -1. Did you?

To rotate counterclockwise 90 degrees we multiply by i. Can we find another complex number we can use with multiplication and rotate 30 degrees or 45 degrees rather than the 90 degrees?

Let us look for the complex number that rotates us 45 degrees c-cl. Look back at your Unit Circle. We are looking at angles that “move” around a circle?! That is ROTATION.

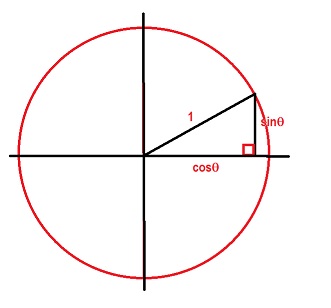
• angle x y
• 30 degrees cos30° sin30°
• 45 degrees cos45° sin45°

And for the complex numbers we have similar table. The x-column above is the real-part of the complex number. The y-column is the imaginary-part.

Graph (1, 0). Using the UNIT CIRCLE for the complex number 1+0i we will have cos0 +isin0. You know the 1 is the cos0 and the 0 is the sin0.

The cos0° +isin0° does = 1+0i. For complex number 1/2+ i(√3)/2 we have cos60° +i sin60°. And what complex number is represented by cos45° +i sin45°?

What can we multiply by that will rotate 45 degrees rather than 90? It is cos45°+i sin45°.

Another use for rotating is developing the trig identities for sums of angles. This was what the video by 3blue1brown wanted us to see. For Cos(A+B) we need the rotation of A and then rotation of B. Recall this is multiplying when we rotate. So what is rotation of A multiplied by rotation of B, of course I mean as a angle or complex number!

(cosA+i sinA) times ( (cosB+i sinB) = ? This is a bit long. If you know the identity already you can use it, but if not then do the multiplying (that is what he did in the video). I know the identity so I prefer to use it! but we are learning something new!!

Find the cos (75°) using the idea above. Change it to rotations that we know! Cos75°= cos(45°+30°) : rotate 45° then rotate 30° then what is the cosine value? Multiply (cos45°+i sin45°) (cos30°+i sin30°) . USE FOIL or distributive property. We get cos45°cos30° +cos45°(i sin45°) +i sin45°(cos30°) +sin45°sin30° i². This simplifies to real part: cos45°cos30° – sin45°sin30° and imaginary part: cos45°(i sin45°) +i sin45°(cos30°). Since we want the cosine of 75°, recall the real part is the cosine (SEE unit circle above), we will only need simplify the cos45°cos30° – sin45°sin30°.

Below is the complete identity for cos(A+B). We determined this from finding the “real” part of the multiplication of (cosA+i sinA)(cosB+i sinB). How could we then find the sin(A+B) ? Let me know.

What is the sin(105°)? What is the cos(105°)? Send me email from Contact page or write in the comments.

We used imaginary numbers to explain trig identities and rotations. Both of these topics are widely used in science, engineering, computer graphics and animations. Perhaps imaginary numbers are more real than we think or maybe they just need a new name! Do you have a suggestion?

Share on Facebook

Tweet