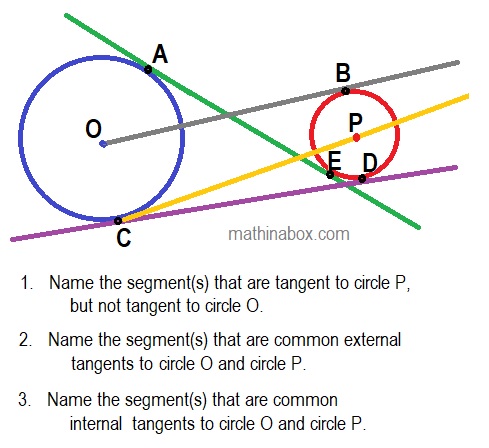
A tangent to a circle is a line which touches the circle at only one point. The point of intersection of the circle and line is called the point of tangency.
For circles P and O in my diagram the centers are points O and P. The other points that are labeled are points of tangency. 1. Can you find the internal and external tangent lines? 2. If the radii OC and PB are drawn in circles O and P then what type angle is created at the point of tangency? acute, right, obtuse or will depend on exact size of the circle.
If you would like to see the tangent and circle “in action” then follow this link to math open reference. The definitions for internal and external tangents are also explained.
For the 3 questions in the diagram there is one line for each question that answers the question. Answers to the 3 questions above in stated order: OB, CD, AE.
The angle created by the tangent and the radius (or diameter) to the point of tangency is a right angle. Thus triangle OBP is a right triangle. Do you see other right triangles (you may draw additional radii)?
Lines of tangency to cylinders and cones have been used for flight paths for flights back into the earth’s atmosphere by various NASA space ships. If you want to know more then research Heading Alignment Cones or TAEM, NASA.
Two of the 4 Phases of TAEM:
- Turns the orbiter towards a point of tangency on the heading alignment cone (HAC) and then flys wings-level until it intercepts the HAC. The tangency point is referred to as “waypoint 1” (WP1). During this phase, the orbiter slows to below Mach 1, at which point the commander takes CSS (control-stick steering), which is the closest thing the shuttle has to a “manual” mode.
- Heading Alignment: Guides the orbiter around a virtual “cone” (see diagram below) until it is in alignment with the runway. It’s not really a cone, mathematically speaking, but it’s the easiest way to visualize it.
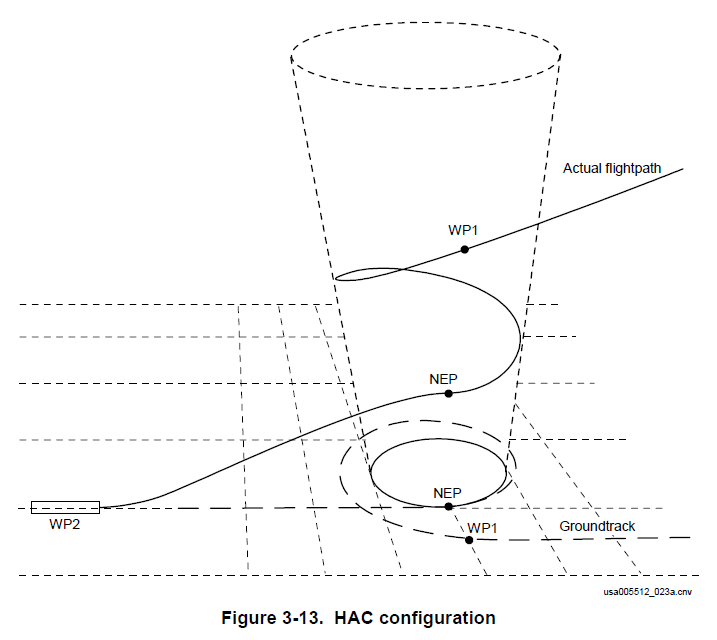
For more info for aviation see this link at stackexchange.com