The question to answer: (Original Post for this question is here.) Which two of the 6 cosine functions below are “exact copies” except for their placement on the x-y axes? Which ones, that is, are translations of each other. Translation means the shape, figure, graph we are considering has been moved vertically or horizontally or both.
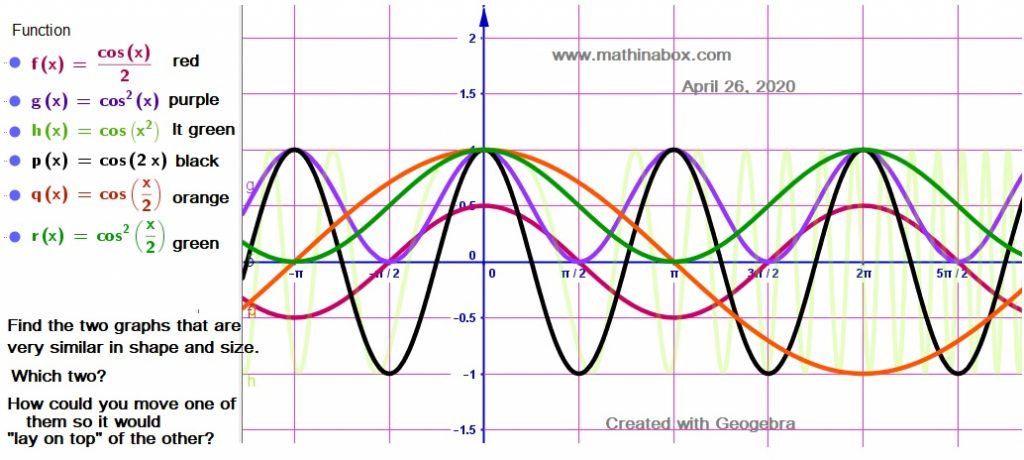
Decide their equation or name (or color). The two functions that are translations are r and f or colors are green and red. You can move the red one how much vertically so that it rests on the green one?
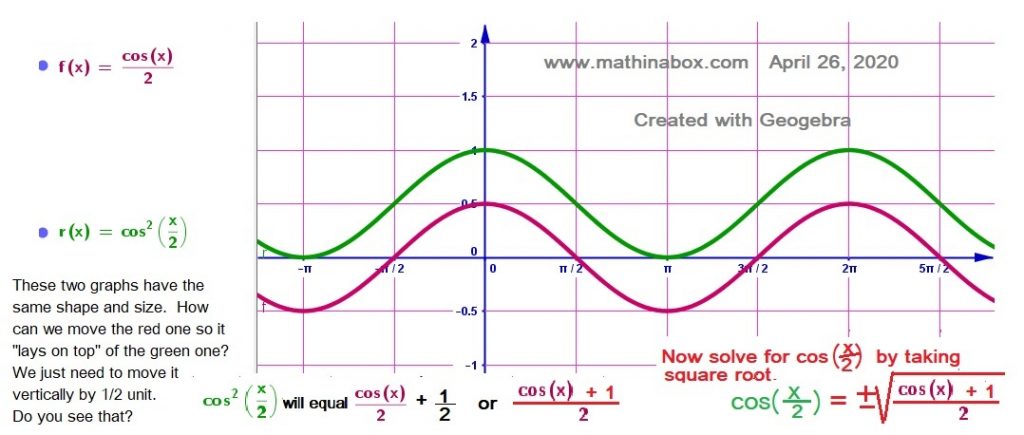
The cosine function r(x) we see the cosine is squared and the angle halved in green graph.
The cosine function f(x) we see the cosine is halved in red graph. If we move the function f(x) up by 1/2 then we write f(x)+1/2. Thus we know:
We can simplify the expression on the right side with a LCD. Do not bother the angles. Just in case you are a little rusty.
If we find the square root of each side we have an identity that many call the half-angle identity for the cosine function. Perhaps you have studied it or have been required to memorize it!
The plus or minus must be determined once you know which quadrant the terminal side of the angle x/2 lies within.
Questions? Oh, Let me ask one : Find the cosine of 112.5 degrees or 5pi/8, without using a calculator! Use the identity above.
Send me you answers using the contact page. Question in the comment box.