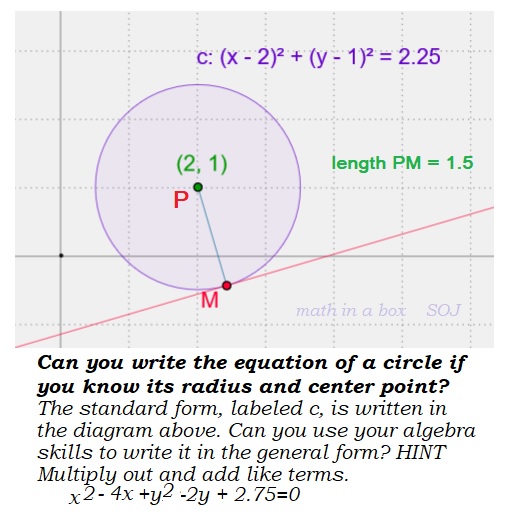
The standard form of the equation of the circle is: (x – h)2 + (y – k)2 = r2 where the r is the radius and the point (h, k) is the center. If the center of the circle is the origin (0, 0), then the equation becomes x2 + y2 = r2. I am sure you know (x- 0)2 =x2 and (y- 0)2 =y2
Notice we have subtraction inside the parentheses, but addition between them!
If the center is point ( 2, -5) then that means h = 2 and k= -5. Let 15 be the radius of the circle. Our equation becomes
(x – (2) )2 + (y – (-5) )2 = 152 . Simplify inside the parentheses first!
(x – 2)2 + (y +5)2 = 225.
Now let us use algebra to square each pair of parentheses.
Be careful! (x – 2)2 is NOT x2 + 4.
To square these I suggest writing them twice and then multiply. SEE: (x – 2 )(x – 2) = x2 -2x -2x +4 = x2 -4x+4. Now do the same for the (y +5)2 You will have y2 +10y +25.
Add together: x2 – 4x+4 + y2 +10y +25 = 225. And simplify.
x2 -4x + y2 +10y +29= 225 becomes
x2 -4x + y2 +10y -196=0 . This is the GENERAL form of the circle.